[백준 -1260번] DFS와 BFS - JAVA 정리 및 해설
안녕하세요 . 백준 문제풀이겸 해설을 맡은 주인장입니다.
저는 문제를 풀때 꼬리를 물면서 풀기를 좋아합니다. 그래서 DFS와 BFS를 배울때 문제를 풀면서 같이 적용하는 것을 꽤 좋아합니다.
DFS와 BFS는 자료를 탐색할때 사용하는 방법으로 자료 탐색시 노드에따라서 어떤식으로 찾을지에 대해서 방식이라고 생각하면 됩니다.
일단 DFS와 BFS를 알기전에 (물론 몰라도 적용은 가능한게 있지만, 그래도 연계해서 알면 좋습니다.) 먼저 익혀야할 개념은 그래프입니다.
그래프는 사실 트리와 DFS와 같은 탐색문제들에 자주 빈번하게 나오는 문제입니다. 그래서 가장 쉬운 이문제를 통해서 두가지 개념을 동시에 알아 보겠습니다.
(단, 이문제에 적용하는 것이지 고급개념에는 적용하기 어려울 수 있으니 차후에 제가 따로 그래프, DFS, BFS에 대해서 따로 정리할 것 같습니다.)
첫번째로 그래프에 대해서 알아보겠습니다.
그래프는 Vertex(꼭지점)과 그 꼭지점을 이어주는 edge(간선)으로 이루어져있습니다.
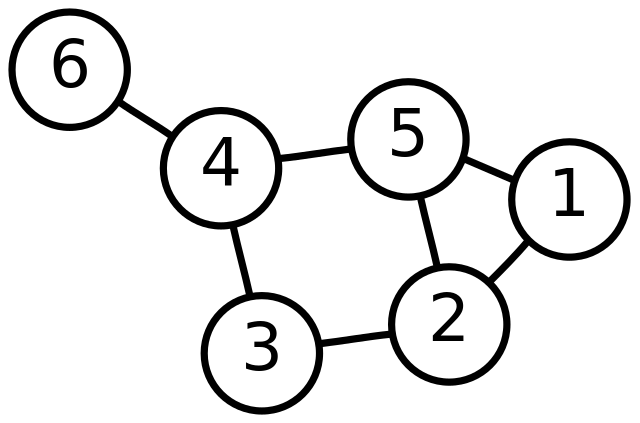
출처: https://ko.wikipedia.org/wiki/%EA%B7%B8%EB%9E%98%ED%94%84
이런 간선들의 연결이 되어있는지 혹은 연결 되지 않았는 것을 판단하는 것이 인접행렬을 이용하거나, 혹은 인접리스트를 이용하는 것이 좋습니다.
1) 인접행렬
사담이긴하지만, 저는 중학교때 행렬을 왜 배우는 가에 대해서 의문이 많았는데, 생각해보니까 지금 이런식으로 배울줄은 상상도 못했죠.
인접행렬은 대부분 이런 꼴을 하고 있습니다.
0 1 0 0 0 1 0
1 0 1 0 0 1 0
0 1 0 1 0 0 0
0 0 0 1 0 1 1
1 1 0 1 0 0 0
0 0 0 1 0 0
이 인접 행렬이 뜻하는 바는
1 2 3 4 5 6
1 0 1 0 0 0 1 0
2 1 0 1 0 0 1 0
3 0 1 0 1 0 0 0
4 0 0 0 1 0 1 1
5 1 1 0 1 0 0 0
6 0 0 0 1 0 0
1번 꼭지점이 k번 꼭지점과 연결이 되있으면 1로 처리를 하거나, 연결이 되있지 않은 선은 0으로 처리해서 이 그래프의 모습을 수식화해서 보여주는 것입니다.
이렇게 그래프를 표현하게되면 장점이 존재하는데,
1차적으로는 배열로 구현하기 때문에 이해가 쉬워서 구현률이 높습니다. 뭐가 뭐에 연결되있는지만 알면, 대략적으로 이 그래프를 인접행렬로 쭉 나열할 수 있습니다.
그리고 예를 들어서 1번 꼭지점과 4번꼭지점이 연결 되있는지를 알고 싶으면, A[1][4]을 통해서 1인지 0인지만 파악하면 연결 되있는 정도를 파악할 수 있는데
치명적인 단점이 존재합니다.
그것은 이 꼭지점의 갯수가 적을때만 가능하다는 점입니다. 그래프는 대부분 시작점에서 도착점을 찾는 방식의 탐색을 많이 하는데(예를 들어서 1번 지점에서 K번지점으로 무엇이 연결되있는지) 그럴려면 A[1][0~K]를 모든 갯수를 탐색해야하는데, 그 곗수는 v가 많아지면 v가 많아질수록 그만큼 탐색 시간이 오래걸리게 되고 매번 연결지점을 찾으려면 v크기만큼 돌아야되기 때문에 시간초과에 걸릴 확률이 정말정말 높습니다. 대부분 난이도가 높은 문제들은 v가 20000이 넘어서 만약 1->3 -> 20000 -> 2처럼 각 꼭지점에서 이 간선이 연결되어있는지 확인을 하려면 그만큼의 시간이 걸린다는 점입니다. 2만씩 5번만 반복해도 10만일텐데 대부분의 문제는 최소 100번은 반복해야될지도 모르고, 더 클 수도 있어서 유의해야합니다.
즉, 이 인접행렬의 경우는 꼭짓점(vertex)가 적은 경우에만 사용하는 것으로 합니다.
2) 인접리스트
인접리스트는 그저 자신의 노드에서 갈 수 있는 노드를 가지고 있다고 생각하면 쉽습니다.
출처:http://manducku.tistory.com/tag/%EC%9D%B8%EC%A0%91%EB%A6%AC%EC%8A%A4%ED%8A%B8
인접리스트는 내가 어디로 갈지를 알려주기만 하니까 즉 어디로 갈지는 내가 찾아서 가보면 됩니다.
만약 1 -> 2 -> 6으로 가고싶다면 1에서는 2로 2에서는 4로 거쳐서 6으로 이동하면 되니까, 내가 그 위치에서 어디로 가야할지 알 수 있는 이정표만 있다고 생각하면 쉽습니다.
즉, 이게 인접행렬에 비해서 수월한점은 실제로 한 지점에서 연결되는 지점만 있기때문에, 사실상 메모리가 차지하는 비율이 상당히 적고 그에따라서 시간복잡도(O(E))가 줄어든다고 생각하면 쉽습니다. 내가 어디 위치로 가기위해서는 그저 노드를 천천히 이동해가면서 파악하면 되니까요.
단, 단점이 있긴합니다. 아까 인접리스트의 장점 A노드와 B노드가 연결되있는지를 알고 싶은 경우에는 인접리스트는 A에는 B가 있는지 B에는 A가 있는지를 파악해서 연결되있는 걸 확인해야하기때문에 직접 다 뒤적거려야하는 단점이 생깁니다.
이렇게 장황하게 그래프를 설명한 이유는 제가 DFS와 BFS를 인접행렬과 인접리스트 두가지를 이용해서 문제를 풀었기때문입니다.
DFS와 BFS에 대해서 설명하는 것은 곧 할 예정입니다.
1) 인접행렬로 구현
package codeBaekJoon; import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.util.Arrays; import java.util.LinkedList; import java.util.Queue; import java.util.StringTokenizer; public class no1260_DFSBFS { static int map[][]; static boolean[] visit; static int n,m,v; public static void dfs(int i){ visit[i] = true; System.out.print(i+" "); for(int j =1; j<n+1; j++){ if(map[i][j] == 1 && visit[j]==false){ dfs(j); // 내가 찾은 경로가 만약에 다른 경로가 있으면 바로 다음 곳으로 이동시키고 만약에 없으면, 다시 리커해서 돌아오는 방식임. } } } public static void bfs(int i){ Queue<Integer> q = new LinkedList<Integer>(); q.offer(i); visit[i] = true; //방문한 위치는 알아야하니까, 그것을 체크하기 위해서 visit가 필요. while(!q.isEmpty()){ int temp = q.poll(); //첫번째 방문한 위치는 빼주기로 한다. System.out.print(temp+" "); for(int k =1; k<=n; k++){ if(map[temp][k]==1 && visit[k]==false){ q.offer(k); visit[k] = true; //true라면 방문을 한거임. ㅇㅇ } } } } public static void main(String[] args) throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); String s = br.readLine(); StringTokenizer st = new StringTokenizer(s," "); n = Integer.parseInt(st.nextToken()); m = Integer.parseInt(st.nextToken()); v = Integer.parseInt(st.nextToken()); map =new int[n+1][n+1]; visit = new boolean[n+1]; for(int j=0; j<n+1;j++){ Arrays.fill(map[j], 0); } Arrays.fill(visit, false); for(int i=0; i<m; i++){ String edge = br.readLine(); StringTokenizer st1 = new StringTokenizer(edge," "); int a = Integer.parseInt(st1.nextToken()); int b = Integer.parseInt(st1.nextToken()); map[a][b]=1; map[b][a]=1; } dfs(v); System.out.println(); Arrays.fill(visit, false); bfs(v); } }
즉, 이 인접행렬의 경우는 꼭짓점(vertex)가 적은 경우에만 사용하는 것으로 합니다.
2) 인접리스트로 구현 -> 단, 어레이리스트 + 트리맵을 통해서 구현.
(bfs는 아직 인접리스트로 구현하지 않았기때문에 인접행렬로 해서 답은 나옵니다. 하지만, 인접리스트로는 구현이 안되어있으므로 이 글이 취소선이 생기면 바뀐겁니다.)
package codeBaekJoon; import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.util.ArrayList; import java.util.Arrays; import java.util.LinkedList; import java.util.Queue; import java.util.StringTokenizer; import java.util.TreeMap; public class no1260_DFSBFS_treeMap { static int map[][]; static boolean[] visit; static ArrayList<TreeMap<Integer, Integer>> arrayList; static int n,m,v; public static void dfs(int i){ visit[i] = true; System.out.print(i+" "); TreeMap<Integer, Integer> tmp = arrayList.get(i); for(int j: tmp.keySet()){ if(visit[j] == false){ dfs(j); } } // for(int j =1; j<n+1; j++){ // if(map[i][j] == 1 && visit[j]==false){ // dfs(j); // 내가 찾은 경로가 만약에 다른 경로가 있으면 바로 다음 곳으로 이동시키고 만약에 없으면, 다시 리커해서 돌아오는 방식임. // } // } } public static void bfs(int i){ Queue<Integer> q = new LinkedList<Integer>(); q.offer(i); visit[i] = true; //방문한 위치는 알아야하니까, 그것을 체크하기 위해서 visit가 필요. while(!q.isEmpty()){ int temp = q.poll(); //첫번째 방문한 위치는 빼주기로 한다. System.out.print(temp+" "); for(int k =1; k<=n; k++){ if(map[temp][k]==1 && visit[k]==false){ q.offer(k); visit[k] = true; //true라면 방문을 한거임. ㅇㅇ } } } } public static void main(String[] args) throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); String s = br.readLine(); StringTokenizer st = new StringTokenizer(s," "); n = Integer.parseInt(st.nextToken()); m = Integer.parseInt(st.nextToken()); v = Integer.parseInt(st.nextToken()); map =new int[n+1][n+1]; visit = new boolean[n+1]; arrayList = new ArrayList<>(); for(int j=0; j<n+1;j++){ Arrays.fill(map[j], 0); arrayList.add(new TreeMap<Integer, Integer>()); } Arrays.fill(visit, false); for(int i=0; i<m; i++){ String edge = br.readLine(); StringTokenizer st1 = new StringTokenizer(edge," "); int a = Integer.parseInt(st1.nextToken()); int b = Integer.parseInt(st1.nextToken()); map[a][b]=1; map[b][a]=1; arrayList.get(a).put(b, a); arrayList.get(b).put(a, b); } dfs(v); System.out.println(); Arrays.fill(visit, false); bfs(v); } }
무난하게 성공을 할 수 있습니다. 감사합니다.
링크: https://www.acmicpc.net/problem/1260
'알고리즘 > 백준 알고리즘' 카테고리의 다른 글
| 백준 답안 공유 - 백준알고리즘 (0) | 2019.01.29 |
|---|---|
| [백준 - 1436번] 영화감독 숌 - JAVA 정리 및 해설 (0) | 2019.01.05 |
| [백준 -1181번] 단어정렬 - JAVA 정리 및 해설 (0) | 2019.01.05 |
| [백준 -10819번] 차이를 최대로 - JAVA 정리 및 해설 (0) | 2018.12.09 |
| [BOJ - 1158번] 조세퍼스 문제 - JAVA 정리 및 해설 (0) | 2018.10.11 |

댓글을 사용할 수 없습니다.